 |
 |
// The simplest version:
// Data structures for depth first search is created internally,
// and depth first search runs internally.
template <class Graph, class DomTreePredMap>
void
lengauer_tarjan_dominator_tree
(const Graph& g,
const typename graph_traits<Graph>::vertex_descriptor& entry,
DomTreePredMap domTreePredMap)
// The version providing data structures for depth first search:
// After calling this function,
// user can reuse the depth first search related information
// filled in property maps.
template <class Graph, class IndexMap, class TimeMap, class PredMap,
class VertexVector, class DomTreePredMap>
void
lengauer_tarjan_dominator_tree
(const Graph& g,
const typename graph_traits<Graph>::vertex_descriptor& entry,
const IndexMap& indexMap,
TimeMap dfnumMap, PredMap parentMap, VertexVector& verticesByDFNum,
DomTreePredMap domTreePredMap)
// The version without depth first search:
// The caller should provide depth first search related information
// evaluated before.
template <class Graph, class IndexMap, class TimeMap, class PredMap,
class VertexVector, class DomTreePredMap>
void
lengauer_tarjan_dominator_tree_without_dfs(
(const Graph& g,
const typename graph_traits<Graph>::vertex_descriptor& entry,
const IndexMap& indexMap,
TimeMap dfnumMap, PredMap parentMap, VertexVector& verticesByDFNum,
DomTreePredMap domTreePredMap)
This algorithm [65,66,67] builds the dominator tree for directed graph. There are three options for dealing the depth first search related values. The simplest version creates data structures and run depth first search internally. However, chances are that a user wants to reuse the depth first search data, so we have two versions.
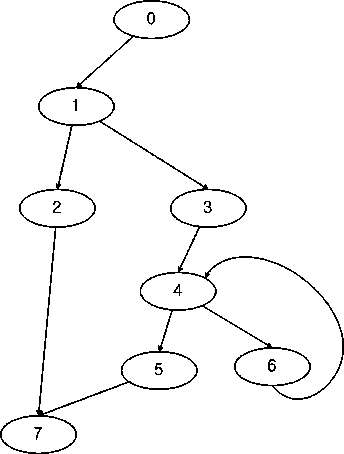
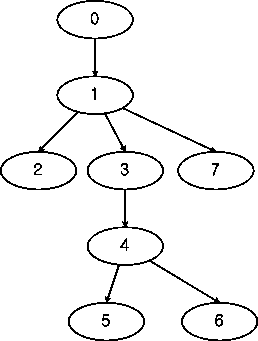
A vertex u dominates a vertex v, if every path of directed graph from the entry to v must go through u. In the left graph of Figure 1, vertex 1 dominates vertex 2, 3, 4, 5, 6 and 7, because we have to pass vertex 1 to reach those vertex. Note that vertex 4 dominates vertex 6, even though vertex 4 is a successor of vertex 6. Dominator relationship is useful in many applications especially for compiler optimization. We can define the immediate dominator for each vertex such that idom(n) dominates n but does not dominate any other dominator of n. For example, vertex 1, 3 and 4 are dominators of vertex 6, but vertex 4 is the immediate dominator, because vertex 1 and 3 dominates vertex 4. If we make every idom of each vertex as its parent, we can build the dominator tree like the right part of Figure 1
An easy way to build dominator tree is to use iterative bit vector algorithm, but it may be slow in the worst case. We implemented Lengauer-Tarjan algorithm whose time complexity is O((V+E)log(V+E)).
Lengauer-Tarjan algorithm utilizes two techniques. The first one is, as an intermediate step, finding semidominator which is relatively easier to evaluate than immediate dominator, and the second one is the path compression. For the detail of the algorithm, see [65].
The graph object on which the algorithm will be applied. The type Graph must be a model of Vertex List Graph and Bidirectional Graph.IN: vertex_descriptor entry
The entry vertex. The dominator tree will be rooted at this vertex.IN: IndexMap indexMap
This maps each vertex to an integer in the range [0, num_vertices(g)). The type VertexIndexMap must be a model of Readable Property Map. The value type of the map must be an integer type. The vertex descriptor type of the graph needs to be usable as the key type of the map.IN/OUT: TimeMap dfnumMap
The sequence number of depth first search. The type TimeMap must be a model of Read/Write Property Map. The vertex descriptor type of the graph needs to be usable as the key type of the TimeMap.IN/OUT: PredMap parentMap
The predecessor map records the parent of the depth first search tree. The PredMap type must be a Read/Write Property Map whose key and value types are the same as the vertex descriptor type of the graph.IN/OUT: VertexVector verticesByDFNum
The vector containing vertices in depth first search order. If we access this vector sequentially, it's equivalent to access vertices by depth first search order.OUT: DomTreePredMap domTreePredMap
The dominator tree where parents are each children's immediate dominator.
The time complexity is O((V+E)log(V+E)).
See test/dominator_tree_test.cpp for an example of using Dijkstra's
algorithm.
| Copyright © 2005 JongSoo Park, Stanford University |
|