File Dependency Example

One of the most common uses of the graph abstraction in computer science is to track dependencies. An example of dependency tracking that is dealt with, on a day to day basis is the compilation dependencies for files in programs that is written. These dependencies are used inside programs such as make or in an IDE such as Visual C++ to minimize the number of files that must be recompiled after some changes have been made. Figure 1 shows a graph that has a vertex for each source file, object file, and library that is used in the killerapp program. The edges in the graph show which files are used in creating other files. The choice of which direction to point the arrows is somewhat arbitrary. As long as the user is consistent in remembering that the arrows mean ``used by'' then things will work out. The opposite direction would mean ``depends on''.
Figure 1: A graph representing file dependencies.
A compilation system such as make has to be able to answer a number of questions:
  1. In order to compile (or recompile) all of the files, what order should that be done it?
  2. What files can be compiled in parallel?
  3. If a file is changed, which files must be recompiled?
  4. Are there any cycles in the dependencies? (which means the user has made a mistake and an error should be emitted)
In the following examples  formulate each of these questions in terms of the dependency graph, and then find a graph algorithm to provide the solution. The graph in Figure 1 will be used in all of the following examples. The source code for this example can be found in the file examples/file_dependencies.cpp.

Graph Setup

To show the construction of the graph. First, these are the required header files: 
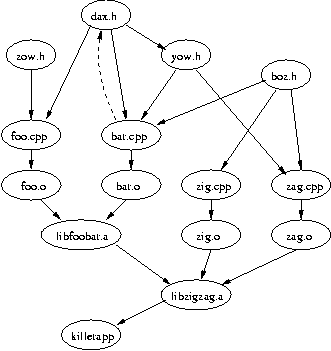
#include <;iostream> // std::cout
#include <utility> // std::pair
#include <boost/graph/graph_traits.hpp>
#include <boost/graph/adjacency_list.hpp>
#include <boost/graph/topological_sort.hpp>
For simplicity construct the graph "by-hand". A compilation system such as make would instead parse a Makefile to get the list of files and to set-up the dependencies. Use the adjacency_list class to represent the graph. The vecS selector means that a std::vector will be used to represent each edge-list, which provides efficient traversal. The bidirectionalS selector means the user wants a directed graph with access to both the edges outgoing from each vertex and the edges incoming to each vertex, and the color_property attaches a color property to each vertex of the graph. The color property will be used in several of the algorithms in the following sections. 
  enum files_e { dax_h, yow_h, boz_h, zow_h, foo_cpp, 
                 foo_o, bar_cpp, bar_o, libfoobar_a,
                 zig_cpp, zig_o, zag_cpp, zag_o, 
                 libzigzag_a, killerapp, N };
  const char* name[] = { "dax.h", "yow.h", "boz.h", "zow.h", "foo.cpp",
                         "foo.o", "bar.cpp", "bar.o", "libfoobar.a",
                         "zig.cpp", "zig.o", "zag.cpp", "zag.o",
                         "libzigzag.a", "killerapp" };

  typedef std::pair<int, int> Edge;
  Edge used_by[] = {
    Edge(dax_h, foo_cpp), Edge(dax_h, bar_cpp), Edge(dax_h, yow_h),
    Edge(yow_h, bar_cpp), Edge(yow_h, zag_cpp),
    Edge(boz_h, bar_cpp), Edge(boz_h, zig_cpp), Edge(boz_h, zag_cpp),
    Edge(zow_h, foo_cpp), 
    Edge(foo_cpp, foo_o),
    Edge(foo_o, libfoobar_a),
    Edge(bar_cpp, bar_o),
    Edge(bar_o, libfoobar_a),
    Edge(libfoobar_a, libzigzag_a),
    Edge(zig_cpp, zig_o),
    Edge(zig_o, libzigzag_a),
    Edge(zag_cpp, zag_o),
    Edge(zag_o, libzigzag_a),
    Edge(libzigzag_a, killerapp)
  };

  using namespace boost;
  typedef adjacency_list<vecS, vecS, bidirectionalS, 
      property<vertex_color_t, default_color_type>
    > Graph;
  Graph g(used_by, used_by + sizeof(used_by) / sizeof(Edge), N);
  typedef graph_traits<Graph>::vertex_descriptor Vertex;

Compilation Order (All Files)

On the first invocation of make for a particular project, all of the files must be compiled. Given the dependencies between the various files, what is the correct order in which to compile and link them? First  formulate this in terms of a graph. Finding a compilation order is the same as ordering the vertices in the graph. The constraint on the ordering is the file dependencies which is represented as edges. So if there is an edge (u,v) in the graph then v better not come before u in the ordering. It turns out that this kind of constrained ordering is called a topological sort. Therefore, answering the question of compilation order is as easy as calling the BGL algorithm topological_sort(). The traditional form of the output for topological sort is a linked-list of the sorted vertices. The BGL algorithm instead puts the sorted vertices into any OutputIterator, which allows for much more flexibility. Here, use the std::front_insert_iterator to create an output iterator that inserts the vertices on the front of a linked list. Other possible options are writing the output to a file or inserting into a different STL or custom-made container. 
  typedef std::list<Vertex> MakeOrder;
  MakeOrder make_order;
  boost::topological_sort(g, std::front_inserter(make_order));
    
  std::cout << "make ordering: ";
  for (  std::cout << std::endl;
The output of this is: 
  make ordering: zow.h boz.h zig.cpp zig.o dax.h yow.h zag.cpp \
  zag.o bar.cpp bar.o foo.cpp foo.o libfoobar.a libzi std::cout << std::endl;
The output of this is: 
  make ordering: 

Another question the compilation system might need to answer is: what  files can be compiled simultaneously? This would allow the system to spawn threads and 
utilize multiplParallel Compilation . Another question the compilation system might need to answer is: what files can be compiled simultaneously? This would allow the 
system to spawn threads and utilize multiple processors to speed up the build.This question can also be put in a slightly different way: what is the earliest time that a file 
can be built assuming that an unlimited number of files can be built at the same time? The main criteria for when a file can be built is that all of the files it depends on must
already be built. To simplify things for this example, assume that each file takes 1 time unit to build (even header files). For parallel compilation ,it is possible to build all of 
the files corresponding to vertices with no dependencies, e.g., those that have an in-degree of 0, in the first step. For all other files, the main observation for determining 
the ``time slot'' for a file is that the time slot must be one more than the maximum time-slot of the files it depends on.

Start by creating a vector time that will store the time step at which each file can be built. Initialize every value with time step zero.
  std::vector<int> time(N, 0);




To visit the vertices against in topological 
order, from those files that need to be built first until those that need to be 
built last. However, instead of printing out the order immediately, compute the 
time step in which each file should be built based on the time steps of the 
files it depends on. Consider those files whose in-degree is greater than zero.


   
    for (i = make_order.begin(); i != make_order.end(); ++i) {   


      if (in_degree (*i, g) > 0) {

        Graph::in_edge_iterator j, j_end;

        int maxdist = 0;

        for (tie(j, j_end) = in_edges(*i, g); j != j_end; ++j)

          maxdist = std::max(time[source(*j, g)], maxdist);

        time[*i]=maxdist+1;

      }ame    }



Last,output the time-slot that is calculated for each vertex.




  std::cout << "parallel make ordering, " << std::endl
       << "  vertices with same group number" << td::endl
       << "  can be made in parallel" << std::endl << std::endl;
  for (boost::tie(i, iend) = vertices(g); i != iend; ++i)
     std::cout << "time_slot[" << name[*i] << "] = " << time[*i] << std::endl;


The output is:


  parallel make ordering, = 2
  time_slot[bar.cpp] = 2
  time_slot[bar.o] = 3
  time_slot[lib  time_slot[dax.h] = 0
  time_slot[yow.h] = 1
  time_slot[boz.h] = 0
  time_slot[zow.h] = 0
  time_slot[foo.cpp] = 1
  time_slot[foo.o] = 2
  time_slot[bar.cpp] = 2
  time_slot[bar.o] = 3
  time_slot[libfoobar.a] = 4
  time_slot[zig.cpp] = 1
  time_slot[zig.o] = 2
  time_slot[zag.cpp] = 2
  time_slot[zag.o] = 3
  time_slot[libzigzag.a] = 5
  time_slot[killerapp] = 6








 
	Cyclic Dependencies





	
   Another question the 
	compilation system needs to be able to answer is whether there are any 
	cycles in the dependencies. If there are cycles, the system will need to 
	report an error to the user so that the cycles can be removed. One easy way 
	to detect a cycle is to run a depth-first search, and if the search runs 
	into an already discovered vertex (of the current search tree), then there 
	is a cycle. The BGL graph search algorithms (which includes 
	depth_first_search()) are all extensible via the visitor mechanism. A 
	visitor is similar to a function object, but it has several methods instead 
	of just the one operator(). The visitor's methods are called at certain 
	points within the algorithm, thereby giving the user a way to extend the 
	functionality of the graph search algorithms. See Section Visitor Concepts 
	for a detailed description of visitors. 

	Create a visitor class and fill in the back_edge() method, which is the 
	DFSVisitor method that is called when DFS explores an edge to an already 
	discovered vertex. A call to this method indicates the existence of a cycle. 
	Inheriting from dfs_visitor<> provides the visitor with empty versions of 
	the other visitor methods. Once the visitor is created, construct and object 
	and pass it to the BGL algorithm. Visitor objects are passed by value inside 
	of the BGL algorithms, so the has_cycle flag is stored reference in this 
	visitor.

	

	struct cycle_detector : public dfs_visitor<>

	{

	cycle_detector( bool& has_cycle) 

	: _has_cycle(has_cycle) { }

	

	template <class Edge, class Graph>

	void back_edge(Edge, Graph&) {

	_has_cycle = true;

	}

	protected:

	bool& _has_cycle;

	};

	Now, invoke the BGL depth_first_search() algorithm and pass in the cycle 
	detector visitor. 

	bool has_cycle = false;

	cycle_detector vis(has_cycle);

	boost::depth_first_search(g, visitor(vis));

	std::cout << "The graph has a cycle? " << has_cycle << std::endl;

	

	The graph in Figure 1 (ignoring the dotted line) 
	did not have any cycles, but if a dependency between bar.cpp and dax.h is 
	added there there will be. Such a dependency would be flagged as a user 
	error. 

	add_edge(bar_cpp, dax_h, g);







Copyright © 2000-20011

Jeremy Siek, Indiana University