 |
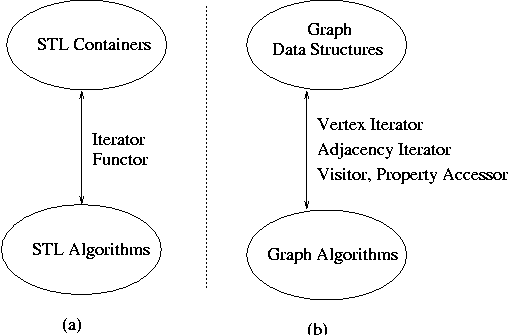
The domain of graph data structures and algorithms is in some respects more complicated than that of containers. The abstract iterator interface used by STL is not sufficiently rich to encompass the numerous ways that graph algorithms may traverse a graph. Instead, formulate an abstract interface that serves the same purpose for graphs that iterators do for basic containers (though iterators still play a large role). Figure 1 depicts the analogy between the STL and the BGL.
The graph abstraction consists of a set of vertices (or nodes), and a set of edges (or arcs) that connect the vertices. Figure 2 depicts a directed graph with five vertices (labeled 0 through 4) and 11 edges. The edges leaving a vertex are called the out-edges of the vertex. The edges {(0,1),(0,2),(0,3),(0,4)} are all out-edges of vertex 0. The edges entering a vertex are called the in-edges of the vertex. The edges {(0,4),(2,4),(3,4)} are all in-edges of vertex 4.
In the following sections, the BGL is used to construct this example graph and manipulate it in various ways. The complete source code for this example can be found in examples/quick_tour.cpp. Each of the following sections discusses a "slice" of this example file. Excerpts from the output of the example program will also be listed.
In this example BGL adjacency_list class is used to demonstrate the main ideas in the BGL interface. The adjacency_list class provides a generalized version of the classic "adjacency list" data structure. The adjacency_list is a template class with six template parameters, though here the user only fill in the first three parameters and use the defaults for the remaining three. The first two template arguments (vecS, vecS) determine the data structure used to represent the out-edges for each vertex in the graph and the data structure used to represent the graph's vertex set (see section Choosing the Edgelist and VertexList for information about the tradeoffs of the different data structures). The third argument, bidirectionalS, selects a directed graph that provides access to both out and in-edges. The other options for the third argument are directedS which selects a directed graph with only out-edges, and undirectedS which selects an undirected graph.
Once the graph type is selected, the graph in Figure 2 can be created by declaring a graph object and filling in edges using the add_edge() function of the MutableGraph interface (which adjacency_list implements). Use the array of pairs edge_array merely as a convenient way to explicitly create the edges for this example.
#include <iostream> // for std::cout
#include <utility> // for std::pair
#include <algorithm> // for std::for_each
#include <boost/graph/graph_traits.hpp>
#include <boost/graph/adjacency_list.hpp>
#include <boost/graph/dijkstra_shortest_paths.hpp>
using namespace boost;
int main(int,char*[])
{
// create a typedef for the Graph type
typedef adjacency_list<vecS, vecS, bidirectionalS> Graph;
// Make convenient labels for the vertices
enum { A, B, C, D, E, N };
const int num_vertices = N;
const char* name = "ABCDE";
// writing out the edges in the graph
typedef std::pair<int, int> Edge;
Edge edge_array[] =
{ Edge(A,B), Edge(A,D), Edge(C,A), Edge(D,C),
Edge(C,E), Edge(B,D), Edge(D,E) };
const int num_edges = sizeof(edge_array)/sizeof(edge_array[0]);
// declare a graph object
Graph g(num_vertices);
// add the edges to the graph object
for (int i = 0; i < num_edges; ++i)
add_edge(edge_array[i].first, edge_array[i].second, g);
...
return 0;
}
Instead of calling the add_edge() function for each edge, use the edge iterator constructor of the graph. This is typically more efficient than using add_edge(). Pointers to the edge_array can be viewed as iterators, so , call the iterator constructor by passing pointers to the beginning and end of the array.
Graph g(edge_array, edge_array + sizeof(edge_array) / sizeof(Edge), num_vertices);
Instead of creating a graph with a certain number of vertices to begin with, it is also possible to add and remove vertices with the add_vertex() and remove_vertex() functions, also of the MutableGraph interface.
Now that a graph is created, the graph can be used interface to access the graph data in different ways. First, all of the vertices in the graph can be accessed using the vertices() function of the VertexListGraph interface. This function returns a std::pair of vertex iterators (the first iterator points to the "beginning" of the vertices and the second iterator points "past the end"). Dereferencing a vertex iterator gives a vertex object. The type of the vertex iterator is given by the graph_traits class. Note that different graph classes can have different associated vertex iterator types, which is why the graph_traits class is needed. Given some graph type, the graph_traits class will provide access to the vertex_iterator type.
The following example prints out the index for each of the vertices in the graph. All vertex and edge properties, including index, are accessed via property map objects. The property_map class is used to obtain the property map type for a specific property (specified by vertex_index_t, one of the BGL predefined properties) and function call get(vertex_index, g) returns the actual property map object.
// ...
int main(int,char*[])
{
// ...
// get the property map for vertex indices
typedef property_map<Graph, vertex_index_t>::type IndexMap;
IndexMap index = get(vertex_index, g);
std::cout << "vertices(g) = ";
typedef graph_traits<Graph>::vertex_iterator vertex_iter;
std::pair<vertex_iter, vertex_iter> vp;
for (vp = vertices(g); vp.first != vp.second; ++vp.first)
std::cout << index[*vp.first] << " ";
std::cout << std::endl;
// ...
return 0;
}
The output is:
vertices(g) = 0 1 2 3 4
The set of edges for a graph can be accessed with the edges() function of the EdgeListGraph interface. Similar to the vertices() function, this returns a pair of iterators, but in this case the iterators are edge iterators. Dereferencing an edge iterator gives an edge object. The source() and target() functions return the two vertices that are connected by the edge. Instead of explicitly creating a std::pair for the iterators, this time use the tie() helper function. This handy function can be used to assign the parts of a std::pair into two separate variables, in this case ei and ei_end. This is usually more convenient than creating a std::pair and is the method of choice for the BGL.
// ...
int main(int,char*[])
{
// ...
std::cout << "edges(g) = ";
graph_traits<Graph>::edge_iterator ei, ei_end;
for (tie(ei, ei_end) = edges(g); ei != ei_end; ++ei)
std::cout << "(" << index[source(*ei, g)]
<< "," << index[target(*ei, g)] << ") ";
std::cout << std::endl;
// ...
return 0;
}
The output is:
edges(g) = (0,1) (0,2) (0,3) (0,4) (2,0) (2,4) (3,0)
(3,1) (3,4) (4,0) (4,1)
In the next few examples, explore the adjacency structure of the graph from the point of view of a particular vertex. Look at the vertices' in-edges, out-edges,and its adjacent vertices. Encapsulate this in an "exercise vertex" function, and apply it to each vertex in the graph. To demonstrate the STL-interoperability of BGL, the STL for_each() function is used to iterate through the vertices and apply the function.
//...
int main(int,char*[])
{
//...
std::for_each(vertices(g).first, vertices(g).second,
exercise_vertex<Graph>(g));
return 0;
}
Use a functor for exercise_vertex instead of just a function because the graph object will be needed while accessing information about each vertex; using a functor gives a place to keep a reference to the graph object during the execution of the std::for_each(). Also template the functor on the graph type so that it is reusable with different graph classes. Here is the start of the exercise_vertex functor:
template <class Graph> struct exercise_vertex {
exercise_vertex(Graph& g_) : g(g_) {}
//...
Graph& g;
};
The first thing to know in order to write the operator()
method of the functor is the type for the vertex objects of the graph. The
vertex type will be the parameter to the
operator() method. To be
precise, we do not deal with actual vertex objects, but rather with vertex
descriptors. Many graph representations (such as adjacency lists) do not
store actual vertex objects, while others do (e.g., pointer-linked graphs). This
difference is hidden underneath the "black-box" of the vertex
descriptor object. The vertex descriptor is something provided by each graph
type that can be used to access information about the graph via the out_edges(),
in_edges(), adjacent_vertices(),
and property map functions
that are described in the following sections. The vertex_descriptor
type is obtained through the graph_traits
class. The typename
keyword used below is necessary because the type on the left hand side of the
scope :: operator
(the
graph_traits<Graph> type)
is dependent on a template parameter
(the Graph
The out-edges of a vertex are accessed with the
out_edges()
function of the IncidenceGraph interface. The
out_edges() function takes two arguments: the first argument is the vertex and the second is
the graph object. The function returns a pair of iterators which provide access
to all of the out-edges of a vertex (similar to how the
vertices()
function returned a pair of iterators). The iterators are called out-edge
iterators and dereferencing one of these iterators gives an edge
descriptor object. An edge descriptor plays the same kind of role as the
vertex descriptor object, it is a "black box" provided by the graph
type. The following code snippet prints the source-target pairs for each
out-edge of vertex v.
The
in_edges()
function of the BidirectionalGraph
interface provides access to all the in-edges of a vertex through in-edge
iterators. The in_edges() function is only
available for the
adjacency_list
if bidirectionalS
is supplied for the Directed template
parameter. There is an extra cost in space when bidirectionalS is
specified instead of
directedS.
Given the out-edges of a vertex, the target vertices of these edges are adjacent
to the source vertex. Sometimes an algorithm does not need to look at the edges
of the graph and only cares about the vertices. Therefore the graph interface
also includes the adjacent_vertices()
function of the AdjacencyGraph interface which
provides direct access to the adjacent vertices. This function returns a pair of
adjacency iterators. Dereferencing an adjacency iterator gives a vertex
descriptor for an adjacent vertex.
BGL attempts to be as flexible as possible in terms of accommodating how
properties are attached to a graph. For instance, a property such as edge weight
may need to be used throughout a graph object's lifespan and therefore it would
be convenient to have the graph object also manage the property storage. On the
other hand, a property like vertex color may only be needed for the duration of
a single algorithm, and it would be better to have the property stored
separately from the graph object. The first kind of property is called an internally
stored property while the second kind is called an externally stored
property. BGL uses a uniform mechanism to access both kinds of properties
inside its graph algorithms called the property map interface, described
in Section Property Map Concepts. In addition,
the PropertyGraph concept defines the interface
for obtaining a property map object for an internally stored property.
The BGL adjacency_list
class allows users to specify internally
stored properties through plug-in template parameters of the graph class. How to
do this is discussed in detail in Section Internal
Properties. Externally stored properties can be created in many different
ways, although they are ultimately passed as separate arguments to the graph
algorithms. One straightforward way to store properties is to create an array
indexed by vertex or edge index. In the
adjacency_list
with vecS
specified
for the
VertexList
template parameter, vertices are
automatically assigned indices, which can be accessed via the property map for
the vertex_index_t. Edges are
In the following example, a graph is
constructed and applied dijkstra_shortest_paths()..
The complete source code for the example is in
examples/dijkstra-example.cpp.Dijkstra's algorithm computes the shortest distance from the starting vertex to
every other vertex in the graph. Dijkstra's algorithm requires that a weight property is associated with each
edge and a distance property with each vertex. Here an internal property
for the weight and an external property for the distance is used. For the weight
property , the property class is used and
int is
specified as the type
used to represent weight values and edge_weight_t
for the property tag
(which is one of the BGL predefined property tags). The weight property is then
used as a template argument for adjacency_list.
The listS and
vecS types are selectors that determine the
data structure used inside the adjacency_list
(see Section
Choosing
the Edgelist
and
VertexList). The directedS type
specifies that the graph should be directed (versus undirected). The following
code shows the specification of the graph type and then the initialization of
the graph. The edges and weights are passed to the graph constructor in the form
of iterators (a pointer qualifies as a RandomAccessIterator).
For the external distance property a
std::vectorr
Often times an algorithm in a library almost does what you need, but
not quite. For example, in the previous section we used Dijkstra's algorithm to
calculate the shortest distances to each vertex, but perhaps we also wanted to
record the tree of shortest paths. One way to do this is to record the
predecessor (parent) for each node in the shortest-paths tree. It would be nice if we could avoid rewriting Dijkstra's algorithm, and just
add that little bit extra needed to record the predecessors
[1]. In the STL,
this kind of extensibility is provided by functors, which are optional
parameters to each algorithm. In the BGL this role is fulfilled by visitors.
A visitor is like a functor, but instead of having just one "apply" method,
it has several. Each of these methods get invoked at certain well-defined points
within the algorithm. The visitor methods are explained in detail in Section
Visitor Concepts.
The BGL provides a number of visitors for some common tasks including a
predecessor recording visitor. The user is encouraged to write his or her own
visitors as a way of extending the BGL. Here we will take a quick look at the
implementation and use of the predecessor recorder. Since we will be using the
dijkstra_shortest_paths() algorithm, the visitor we create must be a
Dijkstra Visitor.
The job of recording the predecessors is quite simple. When Dijkstra's
algorithm relaxes an edge (potentially adding it to the shortest-paths tree) ,
record the source vertex as the predecessor of the target vertex. Later, if the
edge is relaxed again the predecessor property will be overwritten by the new
predecessor. Here, use the put() function associated with the
property map to record the predecessor. The
edge_filter
of the visitor
tells the algorithm when to invoke the explore() method. In this case
the user only wants to be notified about edges in the shortest-paths tree so specify
tree_edge_tag.
As a finishing touch,create a helper function to make it more convenient
to create predecessor visitors. All BGL visitors have a helper function like
this.
Now the record_predecessors
in
Dijkstra's algorithm is ready to use. Luckily, BGL's Dijkstra's algorithm is already
equipped to handle visitors, so, just pass in the new visitor. In
this example there is only one visitor which needs to be used, but the BGL is also
equipped to handle the use of multiple visitors in the same algorithm
(see Section Visitor Concepts).
template <class Graph> struct exercise_vertex {
//....
typedef typename graph_traits<Graph>
::vertex_descriptor Vertex;
void operator()(const Vertex& v) const
{
//...
}
//...
};
Out-Edges, In-Edges, and Edge Descriptors
template <class Graph> struct exercise_vertex {
//...
void operator()(const Vertex& v) const
{
typedef graph_traits<Graph> GraphTraits;
typename property_map<Graph, vertex_index_t>::type
index = get(vertex_index, g);
std::cout << "out-edges: ";
typename GraphTraits::out_edge_iterator out_i, out_end;
typename GraphTraits::edge_descriptor e;
for (tie(out_i, out_end) = out_edges(v, g);
out_i != out_end; ++out_i) {
e = *out_i;
Vertex src = source(e, g), targ = target(e, g);
std::cout << "(" << index[src] << ","
<< index[targ] << ") ";
}
std::cout << std::endl;
//...
}
//...
};
For vertex 0 the output is:
out-edges: (0,1) (0,2) (0,3) (0,4)
template <class Graph> struct exercise_vertex {
//...
void operator()(const Vertex& v) const
{
//...
std::cout << "in-edges: ";
typedef typename graph_traits<Graph> GraphTraits;
typename GraphTraits::in_edge_iterator in_i, in_end;
for (tie(in_i, in_end) = in_edges(v,g);
in_i != in_end; ++in_i) {
e = *in_i;
Vertex src = source(e, g), targ = target(e, g);
std::cout << "(" << index[src] << "," << index[targ] << ") ";
}
std::cout << std::endl;
//...
}
//...
};
For vertex 0 the output is:
in-edges: (2,0) (3,0) (4,0)
Adjacent Vertices
template <class Graph> struct exercise_vertex {
//...
void operator()(Vertex v) const
{
//...
std::cout << "adjacent vertices: ";
typename graph_traits<Graph>::adjacency_iterator ai;
typename graph_traits<Graph>::adjacency_iterator ai_end;
for (tie(ai, ai_end) = adjacent_vertices(v, g);
ai != ai_end; ++ai)
std::cout << index[*ai] << " ";
std::cout << std::endl;
}
//...
};
For vertex 4 the output is:
adjacent vertices: 0 1
Adding Some
Color to the Graph
typedef adjacency_list<listS, vecS, directedS,
no_property, property<edge_weight_t, int> > Graph;
typedef graph_traits<Graph>::vertex_descriptor Vertex;
typedef std::pair<int,int> E;
const int num_nodes = 5;
E edges[] = { E(0,2),
E(1,1), E(1,3), E(1,4),
E(2,1), E(2,3),
E(3,4),
E(4,0), E(4,1) };
int weights[] = { 1, 2, 1, 2, 7, 3, 1, 1, 1};
Graph G(edges + sizeof(edges) / sizeof(E), weights, num_nodes);
// vector for storing distance property
std::vector<int> d(num_vertices(G));
// get the first vertexx
Vertex s = *(vertices(G).first);
// invoke variant 2 of Dijkstra's algorithm
dijkstra_shortest_paths(G, s, distance_map(&d[0]));
std::cout << "distances from start vertex:" << std::endl;
graph_traits<Graph>::vertex_iterator vi;
for(vi = vertices(G).first; vi != vertices(G).second; ++vi)
std::cout << "distance(" << index(*vi) << ") = "
<< d[*vi] << std::endl;
std::cout << std::endl;
The output is:
distances from start vertex:
distance(0) = 0
distance(1) = 6
distance(2) = 1
distance(3) = 4
distance(4) = 5
Extending Algorithms with Visitors
template <class PredecessorMap>
class record_predecessors : public dijkstra_visitor<>
{
public:
record_predecessors(PredecessorMap p)
: m_predecessor(p) { }
template <class Edge, class Graph>
void edge_relaxed(Edge e, Graph& g) {
// set the parent of the target(e) to source(e)
put(m_predecessor, target(e, g), source(e, g));
}
protected:
PredecessorMap m_predecessor;
};
template <class PredecessorMap>
record_predecessors<PredecessorMap>
make_predecessor_recorder(PredecessorMap p) {
return record_predecessors<PredecessorMap>(p);
}
using std::vector;
using std::cout;
using std::endl;
vector<Vertex> p(num_vertices(G)); //the predecessor array
dijkstra_shortest_paths(G, s, distance_map(&d[0]).
visitor(make_predecessor_recorder(&p[0])));
cout << "parents in the tree of shortest paths:" << endl;
for(vi = vertices(G).first; vi != vertices(G).second; ++vi) {
cout << "parent(" << *vi;
if (p[*vi] == Vertex())
cout << ") = no parent" << endl;
else
cout << ") = " << p[*vi] << endl;
}
The output is:font>
parents in the tree of shortest paths:
parent(0) = no parent
parent(1) = 4
parent(2) = 0
parent(3) = 2
parent(4) = 3
Notes
[1]a> The new version of Dijkstra's algorithm now includes
a named parameter for recording predecessors, so a predecessor visitor
is no long necessary, though this still makes for a good example.
Copyright � 2000
Jeremy Siek,
Indiana University ([email protected])
![]()